The Foundation of Mathematics as we know it today has a strange and a remarkable history, but one with too many distortions about its origin and too many ‘speculations’ about it true discovers.
Particularly a lot of original Indian theorems and concepts of fundamental mathematics have been incorrectly credited to Europeans, West and in some cases to the Arabs as well.
Three reasons stand out for this. One, because these knowledge bodies were transported from India to the west over periods of time by Europeans and Arabs and were translated heavily in Latin, Arabic [note1] and other native languages. Two, merely because they were presented to the world in an organized form, while Indians were actually practicing them, rather than paying attention to documenting everything neatly. And three, a more deliberate attempt has been made by the prejudice of the Western scholars[1] towards ‘untutored’ ancient Indians, mainly because it was difficult to come to terms the vast knowledge bodies available here when Europe and the Church was still discovering elementary theories.
But today, a lot of evidence is available in the public domain to show that many branches of pure and applied disciplines of science, mathematics, (and including cosmology [2]) not only originated in India but was also pioneered to the extent that it took centuries for the world to realize, understand and translate it.
(For example – Indian astronomic material circulated widely for centuries before passing into medieval Latin texts.)
In Mathematics alone, Numeral system (as this article would argue), arithmetical principles, invention of zero, notions of infinity, the power and place value, decimal systems [3], geometry, algebra, trigonometry, calculus and many other mathematical concepts came from India. And nearly all such complex ideas and theorems and methods travelled abroad, mixed, modified, and interpolated with the ideas of the land it travelled to and were later wrongly attributed to either Greeks or Europeans thereby hiding their Indian origins.
The case of Hindu-Arabic numeral and place value system
One such original Indian product, which has profound significance on the development and evolution of mathematics, is the numeral and place-value system.
It too was transmitted to the Arabs (and later into Europe), studied and suited accordingly to Arabic needs and as a result, what was an original Hindu numeral system, came to be called as Hindu-Arabic numeral system that the world knows of today.
French scholar Pierre-Simon Laplace, in support of it once wrote:
“The ingenious method of expressing every possible number using a set of ten symbols (each symbol having a place value and an absolute value) emerged from India. The idea seems so simple nowadays that its significance and profound importance is no longer appreciated. Its simplicity lies in the way it facilitated calculation and places arithmetic foremost amongst useful inventions. The importance of this invention is more readily appreciated when one considers that it was beyond the two greatest men of Antiquity, Archimedes and Apollonius.” [4]
Distortion of the Hindu numeral system and origin of the Hindu-Arabic Numeral system
To tell a long story short: Hindu–Arabic numeral system (~800 AD) is made up to three things.
Existing Hindu Numeral system (which includes the place-value notation due Aryabhata and use of Zero due to Brahmagupta)
+
Modification of the existing archaic Arabic numeral system by Islamic scholars (key scholar being Al-Uqlidist who documented all his writings into a book) with the help of glyphs from Indian Brahmi numerals (~250 BC)
+
Reproduction of the calculations and results by Arabs scholars to suit Arab way of doing mathematics. Arabs, often call it as ‘Raqam Al-Hind’ or sometimes they still call it as the Hindu numeral system [5]
In short, the ordinary numerals we use today or the Hindu-Arabic numerals, 0, 1,2,3, 4, 5, 6,7, 8,9 were originally from India and were slowly introduced into the West via the Arab world after the Hegira (AD 622). Later, Robert of Chester in 1145 translated his entire work into Latin paving the way for the ‘modified’ Hindu numeral system to reach almost entire Europe. It was used until the sixteenth century as the principal mathematical textbook of European universities. “Arabic” numerals passed from “the Hindus or Persians to the Arabs, then to the Moors in Spain, then finally to the Spanish and the rest of Europe”.
Now, three important things need to be understood in order to provide evidence to the facts stated in this article.
- [A] What, How and why were the modifications done by ‘Al-Uqlidist’?
- [B] To arrive at his formulae and calculations, Al-Uqlidist also referred two prominent books by Islamic scholars. Book 1: The Compendious Book on Calculation by Completion and Balancing, c. 813–833 CE by Muḥammad Khwārizmī (c.780 – c.850) (Latin Translation – Algorithmo de Numero Indorum) and Book 2: Al-Kindi (On the Use of the Hindu Numerals, 830). Were these books any original source of Algebraic knowledge? Or did they borrow too from Indian knowledge available.
- [C] Indian Brahmi numerals were in fact the true precursors to the modern Indian or ‘Hindu-Arabic numeral system’. And this new system has nothing or very little to do with actual Arabic numerals and Math. But did the Brahmi numeral has any foreign borrowing?
Answers to these Questions in details
Kept in the Yeni Gami Library, Istanbul is one of the earliest known and still surviving extant in Arabic called ‘Kitab al-Fusul fi al Hisab al-Hindi’ written by ‘Abu al-Hasan, Ahmad ibn Ibrahim al-Uqlidisi’. Note that the title ‘al-Uqlidisi’ is a nickname that is giving to the person for writing copies for sale, and not an author. The text, containing roughly 230 leaves (folios), shows that al-Uqlidisi must have some experience in teaching arithmetic, but majorly he earned his living by copying. The author claims that the book referenced many other books versed in the ‘Arithmetic of the Indians’ and has met many experts and scholars of that time.
However, al-Uqlidisi’s book is poorly copied, calculations on fractions end abruptly (folio 178), divisions are missing (folio 20) etc. Now, the old-fashioned arithmetic of the Arabs which was called by Muslim authors as ‘Hisaab-al-yadd’ (hand arithmetic or finger arithmetic) was dependent on counting as indicated by fingers. So, it has an inherent limitation that it was unable to express large numbers or fractions. The Sexagesimal scales (from 3rd millennium BC) available at that time was also not of much use because of its complexity and was largely used by astronomers. Now, Al-Uqlidisi, was very much appreciative of the Indian methods – which in his own words was ‘easy, quick, saved the trouble of memorizing and needed little precaution’[Note]
But despite all those methods, Indian Arithmetic was disliked in the Arab world. In the book he wrote (in folio 2b) he explains that it was because it needed the dust abacus / a ‘takht’ (a Persian word which means board)’. Now, in order for his work to be liked i.e. to ‘hide its Indian origin’, he replaced the nine letters of the numerals with the Greek alphabet.
In the book, he writes “if some person dislikes it because it needs a ‘takht’, we say that this is science and art that needs a tool. …..*and later in the same folio he continue to say…’we may hide it also by means we shall mention so that one who sees him that computes with it (with the Indian method) does not know that is it Hindi [6] but thinks that it is Rumi.
Thus, his modification of the India process to suit paper and ink and avoid rubbing out depends largely upon indicating the digits to be preserved by jummal letters of the Arabic alphabet, where those which are to be rubbed out appear in Hindu-Arabic Numerals. These modifications led Hindu arithmetic to enter Islam and Damascus (Capital of the Syrian Arab Republic) with the dust board. Further, Abu-al-Wafu (10th century) gave arithmetic for multiplication and some for division by drawing from Hindu schemes – and he modified it in a way that does not need the ‘takht’, dust, stylus, rubbing off, and hence widely accepted.
Thus, Indian Arithmetic entered Islam with ‘Dust abacus’ and Arabs called it ‘Takht’ and attempts were made to modify this arithmetic from tenth century itself. To Al-Uqlidist, who did explore the Hindu arithmetic in this way, arithmetic was still Hindi which meant two things – Indian and that which is done in the Indian way (i.e. written on a dust board) this expressed in Hindu Arabic numerals.
[Answer to Question B]
1] Consider this book by Khwārizmī, one of the most prominent of mathematics and astronomers of Baghdad: The Compendious Book on Calculation by Completion and Balancing, c. 813–833 CE
The main achievements of this book were [a] how to solve quadratic equations and [b] reduction and balancing (cancelling like terns on either side of the equation).
However, long before him, Baudhāyana Śulbasûtra’ (which were appendices to the Vedas) mainly attributed to Vedic priest ‘Baudhāyana’(800 BCE) while prescribing instructions to construct altars for sacrifices shaped into geometrical figures, had already solutions of linear and quadratic equations, square root of 2 (sutra i.61-2) [7a]. Infact, solution of linear equation came even before that with Brahmagupta in his work Brāhmasphuṭasiddhānta (628 CE).
(Moreover, a method for constructing triples (like a2 + b2 = c2) as fuond in Plimpton 322 clay tablet (1850 BC) is considered as a key achievement of Babylonian mathematics as well when the same existed independently in India but was never credited to the nation.)
The Bakhshali Manuscript (~AD 200) written in India contained an algebraic formula for solving quadratic equations, and quadratic indeterminate equations (originally of type ax/c = y). And the Bakhshali extant manuscript, one must know was never discovered in full. And not just this, the problems contained in it, solutions described, and detailed proofs include a wide range of topics from fractions, square roots, arithmetic, and geometric progressions, solutions of simple equations, simultaneous linear equations, quadratic equations and indeterminate equations of the second degree [22]. Indian mathematician Brahmagupta in his book ‘Brahmasphutasiddhanta’ (628 AD), gave the first explicit (although still not completely general) solution of the quadratic equation ax2 + bx = c, besides giving concrete rules for both positive and negative numbers [7b]
Al-Khwarizmi’s work, De numero indorum (Concerning the Hindu Art of Reckoning), was based presumably on an Arabic translation of Brahmagupta where he gave a full account of the Hindu numerals which was the first to expound the system with its digits 0,1,2,3,….,9 and decimal place value which was a fairly recent arrival from India [8a]. He and his contemporaries such as ‘Abd al-Hamīd ibn Turk were inspired by Brahmagupta [8b] and these concepts existing in India to compose their book and developed formulas. Islam’s Golden Age of science and mathematics (the 9th to 15th Centuries) also saw the development of the complex symmetries used in Islamic temple decorations – all these sourced in some way to the geometric patterns that Khwarizmi’s work was expounding. His strong advocacy of the Hindu numerical system revolutionized Islamic. Another major figures of Islamic mathematic who made several visits to India was al-Biruni. From Arabic translations of some Sanskrit texts, he was familiar with the Indian astronomy and mathematics and he wrote extensively on Indian numerals.
Later, Jewish mathematicians, Chinese mathematician Yang Hui, French René Descartes (1596) and others build up detailed solutions on top of what was already known and existing and were credited with the results as founders of it.
But if mere detailing the solutions should be the criteria to give the credit, then Sanskrit pandit ‘Sridhara’ (750 AD) should be credited with computing the roots of the quadratic equation and solving and not Descartes. But is that the case? No.
So, is it accurate to call ‘Khwarizmi’ as Father of Algebra?
Al-Khwārizmī treatise in Arabic language was translated into Latin in the 12th century with the title Algoritmi de numero Indorum, where “Algoritmi” was the translator’s Latinization of Al-Khwarizmi’s name. The title means “Algoritmi on the numbers of the Indians” and al-jabr”, literally meaning “reunion of broken parts. Giving this etymology, the name Algebra that comes from al-Khwarizmi’s above book (in Persian it is called as Ilm al-jabr) itself has no significance to the subject’s history. The processes of calculation (addition, multiplication, etc.) using these numerals acquired the name of “algorism” because the texts on the processes were associated with the name of Al-Khwar- – izmi. Further, Algebra involves dealing with real and complex numbers, equation solving, inequalities, symmetry, simplex and complex structures such as groups, rings, fields etc. whereas Khwarizmi’s book has no such details. In fact, another book ‘The Nine Chapters on the Mathematical Art’, a Chinese mathematics treatise, composed by several generations of scholars from the 10th–2nd century BCE (much before Khwārizmī) contains mathematical proofs for areas of various shapes, such as rectangles, triangles, trapezoids, and circles [9] which itself was inspired by Indian writings available to Chinese at that time.
Now, to prove that the Indian numeral system did infact was original, let’s ask and answer the question ‘Does the Brahmi script itself has any non-indigenous or Semitic borrowing?
Whether Brahmi (1000 BC), derived from Sanskrit presumably (>5000BC) was of truly Indian origin in all its parts or whether some part of it was borrowed from some other script is important to understand because the entire Hindu-Arabic system – which should be called as ‘Hindi’ system of numerals with the ‘Glyph’ notation – depends on it and the glyphs notation comes from Brahmi script.
i.e..
- Is Brahmi Script having Indian origin?
- is it of Semitic borrowing (originated outside India)?
Westerners systematically, over the ages, could not convince themselves of the theory of indigenous origin and favored Semitic borrowing. Studies suggest that most proponents of the indigenous view are Indian scholars, whereas the theory of Semitic origin is held by “nearly all” Western scholars. So, who is right?. Alexander Cunningham states that Brahmi characters were majorly derived from a pictographic principle based on the human body. Now, this makes sense as the basis of the Phonology of Devanagari and other India scripts – which are part of the Brahmic family and deriving from Sanskrit is based on the similar principles in terms of how the vowels and consonants are arranged in the script and are spoken. i.e. kaṇṭhya (Guttural) – > talavya (Palatal) – > Oṣṭhya (Labial) and so on.
While one of the key scholars upon whose writing scholars advocated the other theory is Georg Buhler. One of the main evidences they present is that another script Kharoshi, which was present at that time is a definitive adaptation of Semitic, and hence Brahmi, whose origin in uncertain, should have borrowed from other scripts too [10]
But the connection between Brahmi and Semitic remains unclear to this date. And the fact that Brahmi originated before the 3rd century BCE (much before Kharoshi), based on the archaeological findings in Sri Lanka (during late 20th century) could confirm Brahmi had a complete independent origin, the one rooted in Vedic literature (the Brahmana).
Ironically, Georg Buhler himself, in his book [11] mentioned that out of the five theories in which only one favored indigenous origin, he favored the indigenous one. (refer a snapshot below from his book). The debate is yet not settled but scholars are now coming to terms with its indigenous origin slowly.

Brahmi script, with its own numerals, consonants and vowels is one of the world’s most influential writing tradition [12], a direct ancestor of around 198 scripts including the world’s biggest family of Indo-European languages, that includes some 449 languages [13,14] and dialects and is spoken by roughly half of the world’s population today. It is Brahmi which ultimately provided the graphic forms for the Hindu–Arabic numeral system now used through most of the world [15]
French mathematician Georges Ifrah, wrote in his book “Universal History of Numbers” [16]
‘..the discovery of zero and the place-value system were inventions unique to the Indian civilization. As the Brahmi notation of the first nine whole numbers (incontestably the graphical origin of our present-day numerals and of all the decimal numeral systems in use in India, Southeast and Central Asia and the Near East) was autochthonous and free of any outside influence, there can be no doubt that our decimal place-value system was born in India and was the product of Indian civilization alone.
But, unfortunately, the minds of our current generation, including Indian scholars of post-imperialistic world, are trained by what has been written by foreign scholars who are seldom aware of the facts, and hence the reason why there have been multiple theories and views among themselves, and not one with a evidence that could contradict the other.
Since we are talking about the foundation of mathematics, let’s look at the very few other classic examples where transportation of original Indian knowledge to West and Europe was the basis as to why theorems and concepts are named after the west and Europeans and not Indians.
- Boolean algebra : Is due to English mathematician George Boole from the book The Mathematical Analysis of Logic(1847), when infact, Sanskrit grammarian, Pāṇini’s Vyakaran (c. 520–460 BCE) includes early use of Boolean logic, the null operator, context free grammars (which are a basic of today’s XML languages) and includes a precursor of the Backus–Naur form (used in the description programming languages) [17]
- Fibonacci series [note 2]: Considered to be the most talented Italian mathematician of the Middle Ages, Fibonacci (AD 1170) introduced Europe to the sequence of Fibonacci numbers, and hence the series named after him. But the truth is Pingala’s Maatraameru (Mountain of Cadence) work in the Chhandah-shastra (Art of Prosody) contains the basic ideas of Fibonacci numbers (roughly 450 BC) [18], along with other critical results such as binary numeral system, binomial theorem with the help of Sanskrit Prosody. Fibonacci was also among those who popularized the Hindu–Arabic numeral system in the Western World primarily through his composition in 1202 of Liber Abaci(Book of Calculation) [19]
- Pythagoras theorem: The world still credits Euclid (~300 BC) with Pythagoras theorem whereas in Baudhayana Sulbasutra and Katyayana Sulbasutra, five hundred years before Euclid (800 BC), both special and generalized version of the same theorem exists with details, including other results [20].
- Metric and other systems: Complex measurement systems, architectural, and metallurgical artifacts dating back to 5000 BC [21] existed in India including the timing scale from 10-7 to 1022 much before the knowledge of Egyptians and Mesopotamians. But the credit for the metric system has been given to French Revolution when there was ‘ZERO’ novel metric invention at that time – that which would not have existed before in ancient India.
Comparing the scale of Key achievements of the world, starting from Sumerians (~4000 BC), prominent were in metrology, multiplication tables (2600 BC), geometrical problems and division, sexagesimal number system (~3000 BC), a place value numeral system, finding the area of a triangle and volume of cube. And these became the foundations for some of the achievements of the Babylonian time (~1800 BC) (practiced by the people of Mesopotamia), such as system of mathematics and numerals, sexagesimal (base 60) numeral system that is the basis of today’s 60 seconds in a minute, 60 minutes in an hour, and 360 degrees in a circle concept, Approximation of √2 and few others.
However, all these systems were developed independently in India, with even more complexities and accuracies and some probably existed even before that.
But, without any documents or unreadable evidence, such claims are assumed as myth – even if evidences like these are available, they are brushed aside for we do not bother to react and fight for the truth. The onus really lies on us to study, research and bring forth such marvels of ancient India to the world.
*
Key References and Additional Notes
[1] For an example, a paper below, using a case study on the algebraic solutions to a linear problem details how a biased and prejudiced humanist approach, probably risen from Greek soil, has Influenced the recognition and appreciation of Indian mathematics.
[2] About modern Cosmology : Refer the excerpt here from the book Religion, Learning and Science in the ‘Abbasid Period, edited by M. J. L. Young, J. D. Latham, R. B. Serjeant, Cambridge University Press. An excerpt here : https://books.google.ca/books?id=cJuDafHpk3oC&pg=PA302&redir_esc=y#v=onepage&q&f=false
Astronomical finding in India are vast and humongous and predates all civilizations for example, long before Galileo discovered nine planets, Indians knew about ‘Navgrah’ (or nine planets).
[3] Quoting an article dated 16 May 2007 from Encyclopedia Britannica Online: “A full-fledged decimal, positional system certainly existed in India by the 9th century (AD), yet many of its central ideas had been transmitted well before that time to China and the Islamic world. Indian arithmetic, moreover, developed consistent and correct rules for operating with positive and negative numbers and for treating zero like any other number, even in problematic contexts such as division. Several hundred years passed before European mathematicians fully integrated such ideas into the developing discipline of algebra.
[4] http://www-history.mcs.st-andrews.ac.uk/HistTopics/Indian_mathematics.html
[5] The Hindu-Arabic numerals by David Eugene Smith, Louis Charles Karpinski
[6] Al-Hindi means India or the Indians. Hindi is the adjective form.
[7a] https://en.wikipedia.org/wiki/Baudhayana_sutras#cite_ref-Plofker_27_1-0 and Mathematics in India by By Kim Plofker
[7b] Bradley, Michael. The Birth of Mathematics: Ancient Times to 1300, p. 86 (Infobase Publishing 2006).
[8a] http://www.ms.uky.edu/~carl/ma330/project2/al-khwa21.html
[8b] K Shankar Shukla, Early Hindu methods in spherical astronomy, Ganita 19 (2) (1968), 49-72 mentions that Brahmagupta is also probably the earliest astronomer to have employed the theory of quadratic equations and the method of successive approximations to solving problems in spherical astronomy
[9] https://en.wikipedia.org/wiki/The_Nine_Chapters_on_the_Mathematical_Art
[10] https://www.ancient.eu/Brahmi_Script/
[11] https://ia802702.us.archive.org/23/items/onoriginofindian00buhliala/onoriginofindian00buhliala.pdf
[12] Palaeolinguistic Profile of Brahmi Script’ by Dilip Rajgor; (2000)
[13] “Ethnologue report for Indo-European”. Ethnologue.com.
[14] Quiles, Carlos (June 2017). “Indo-European demic diffusion model”(PDF) (2nd ed.). Badajoz: Universidad de Extremadura. Retrieved March 24, 2018.
[15] Indian Epigraphy: A Guide to the Study of Inscriptions in Sanskrit, Prakrit, and the other Indo-Aryan Languages’ by Richard Salomon. Oxford University Press, Dec. 10, 1998 – Religion – 400 pages
[16] https://www.indiancentury.com/math.htm
[17] https://dl.acm.org/citation.cfm?doid=363162.363165 and https://www.infinityfoundation.com/mandala/t_es/t_es_rao-t_syntax.htm
[18] http://people.sju.edu/~rhall/mathforpoets.pdf
[19] http://www.halexandria.org/dward093.htm
[20] http://www-groups.dcs.st-and.ac.uk/history/HistTopics/Indian_sulbasutras.html
[21] https://ipfs.io/ipfs/QmXoypizjW3WknFiJnKLwHCnL72vedxjQkDDP1mXWo6uco/wiki/History_of_measurement_systems_in_India.html
[22] G. R. Kaye, The Bakhshâlî Manuscript— A Study in Mediaeval Mathematics by Bibhutibhusan Datta
[Other references]
- https://en.wikipedia.org/wiki/History_of_the_Hindu%E2%80%93Arabic_numeral_system
- https://en.wikipedia.org/wiki/Brahmagupta#cite_note-YoungLatham2006-12
- https://en.wikipedia.org/wiki/Indian_mathematics#cite_note-4
- https://en.wikipedia.org/wiki/Plimpton_322
- https://en.wikipedia.org/wiki/History_of_mathematics#cite_ref-130
- https://en.wikipedia.org/wiki/Algorism#cite_note-5
- https://www.sciencedirect.com/science/article/pii/031508609090048I
- https://en.wikipedia.org/wiki/The_Compendious_Book_on_Calculation_by_Completion_and_Balancing#cite_note-4
- https://en.wikipedia.org/wiki/Brahmi_numerals
- https://en.wikipedia.org/wiki/Muhammad_ibn_Musa_al-Khwarizmi#cite_note-43
[Note] Some section of the above paragraph and taken are taken as it is from the JOURNAL ARTICLE ‘The Earliest Extant Arabic Arithmetic: Kitab al-Fusul fi al Hisab al-Hindi of Abu al-Hasan, Ahmad ibn Ibrahim al-Uqlidisi’ by A. S. Saidan. Vol. 57, No. 4 (Winter, 1966) Published by: The University of Chicago Press on behalf of The History of Science Society
[Note 1] Brahmagupta’s texts were translated into Arabic by Muhammad al-Fazari, Persian Mathematician Al-Khwarizmi (800–850 CE) wrote a text called al-Jam wal-tafriq bi hisal-al-Hind (Addition and Subtraction in Indian Arithmetic), which was translated into Latin in the 13th century as Algorithmi de numero indorum. And through these translated texts, the decimal number system and Brahmagupta’s algorithms for arithmetic have spread throughout the world.
[Note 2] ‘to the nine digits of the Hindus’ Fibonacci himself stated ‘the knowledge of the art very much appealed to me’.. and goes on further to state that ..‘the art of Pythagoras, I considered as almost a mistake in respect to the method of the Hindus…’






































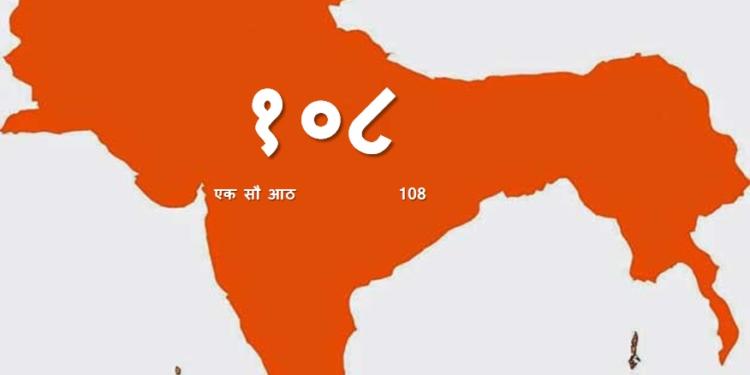














The true origins of mathematics was hidden by the liars from Babylon who travelled to Europe/UK approx 2000 years ago.They have been treating the glory of India with contempt to this day.
Well Iv’e known for some years of the Indian origin (and possibly more oriental origins too) of numerical symbols and some of their uses and how Muslims want to claim them as their own, but I have never been told, read or taught that they were a product of the West so I am surprised to read that we Westerners are being blamed for that. I’m just wondering who these guilty persons may be.